

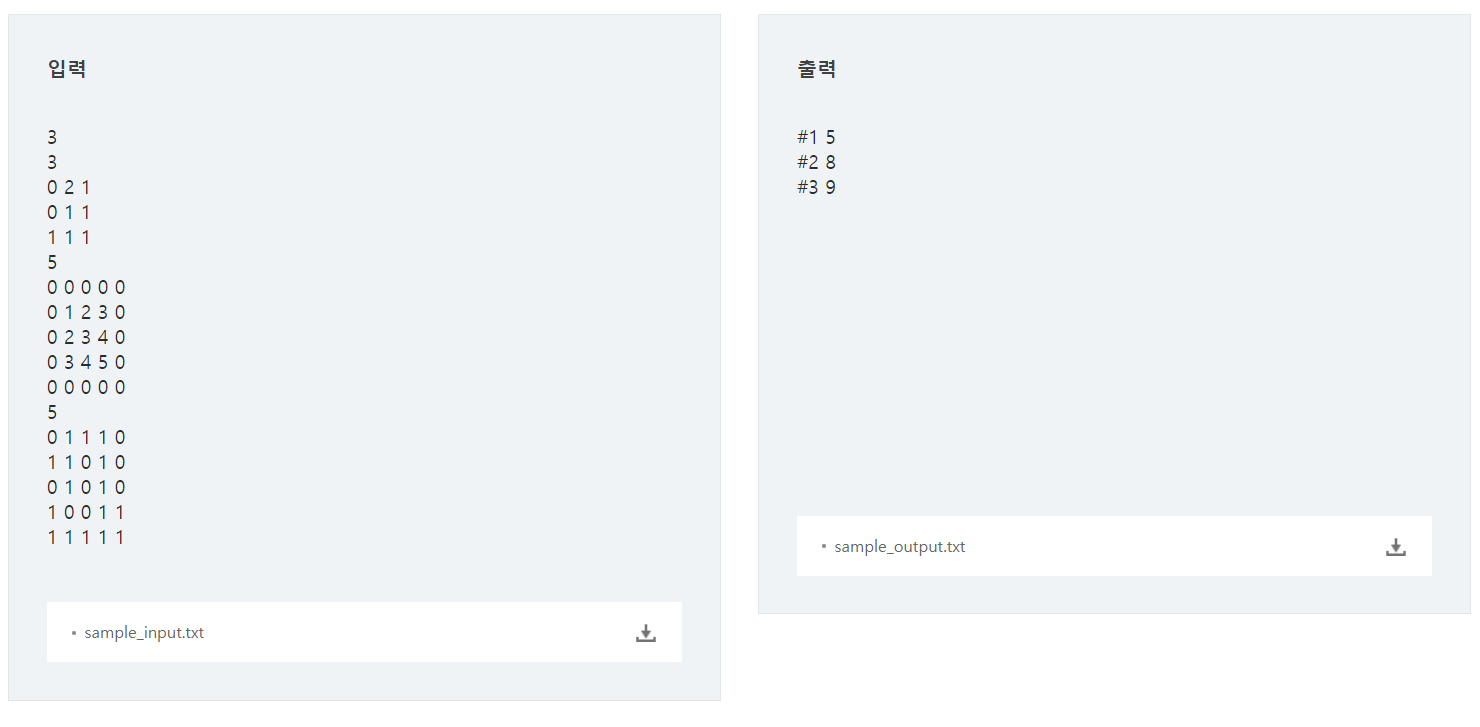
문제풀이
- 2차원 배열의 특정 위치에서 부터 인접 좌표들로 이동을 하면서 최소비용을 구하는 문제
- 가중치가 없다면 단순 bfs로 해결할 수 있음.
- 문제에서는 현재좌표의 높이와 새로운 좌표의 높이 차이가 있다면 ( 새로운 좌표가 높다면) 그 높이 만큼을 가중치로 계산함
- 시작점 (0,0)에서 BFS 탐색을 하면서 각 인접 좌표 (상하좌우)에 대해 간선완화를 진행
- 한 좌표의 상하좌우에 있는 새로운 좌표 계산
- 각 좌표가 범위내인지 확인
- 새로운 좌표의 높이가 현재의 높이보다 높다면 그 차이를 가중치로 계산
- 높이 차이가 없거나 새좌표가 더 낮으면 가중치는 1 (기본 비용)
- 새로운 좌표의 현재까지의 최소비용(시작점에서 부터의 최소비용)가 현 좌표를 찍고 가는 것 보다 높으면 새로운 비용으로 갱신
- 새좌표의 최소비용 > 현좌표 최소비용 + (현-새 높이차) 면 갱신
- 새 좌표를 큐에 넣기 : 그 좌표 부터 새 좌표를 찾기 위해서
- 반복이 끝나고 N-1,N-1에 있는 비용이 최소비용

소스코드(python)
def find():
dr = [-1,0,1,0]
dc = [0,1,0,-1]
INF = 100000000 #큰값
dist = [[INF]*N for i in range(N)] #최단거리 배열 (2차원)
dist[0][0] = 0 #시작 값을 0으로
#시작점에서 상하좌우로 탐색 -> 또 거기서 상하좌우 탐색 : bfs 탐색
q = [] #큐 준비
q.append((0,0)) #시작점 큐에 넣기
while q:
t = q.pop(0)
for k in range(4): #사방탐색
nr = t[0] + dr[k]
nc = t[1] + dc[k]
if nr>=0 and nr < N and nc >= 0 and nc < N:
diff = 0 #높이차이
if Map[nr][nc] > Map[t[0]][t[1]]: #높이 차이가 나면
diff = Map[nr][nc] - Map[t[0]][t[1]] #그 높이 차이가 가중치
#새롭게 갈 좌표의 최단거리가 현위치의 최단거리 + 현위치-새위치 가중치 + 1(기본적인 비용)
if dist[nr][nc] > dist[t[0]][t[1]] + diff +1:
dist[nr][nc] = dist[t[0]][t[1]] + diff + 1
q.append((nr,nc))
return dist[N-1][N-1] #도착점의 값 리턴
T = int(input())
for tc in range(1,T+1):
N = int(input())
Map = [list(map(int,input().split())) for _ in range(N)]
print("#{} {}".format(tc, find()))
'알고리즘 > SWEA' 카테고리의 다른 글
| [SWEA] 1859.백만장자 프로젝트 - python (2) | 2021.02.25 |
|---|---|
| [SWEA] 5521. 상원이의 생일파티 - python (0) | 2020.07.24 |
| [SWEA] 1949. 등산로 조성 (python) (0) | 2020.07.08 |